Los problemas de matemáticas más difíciles y virales de los últimos 12 meses
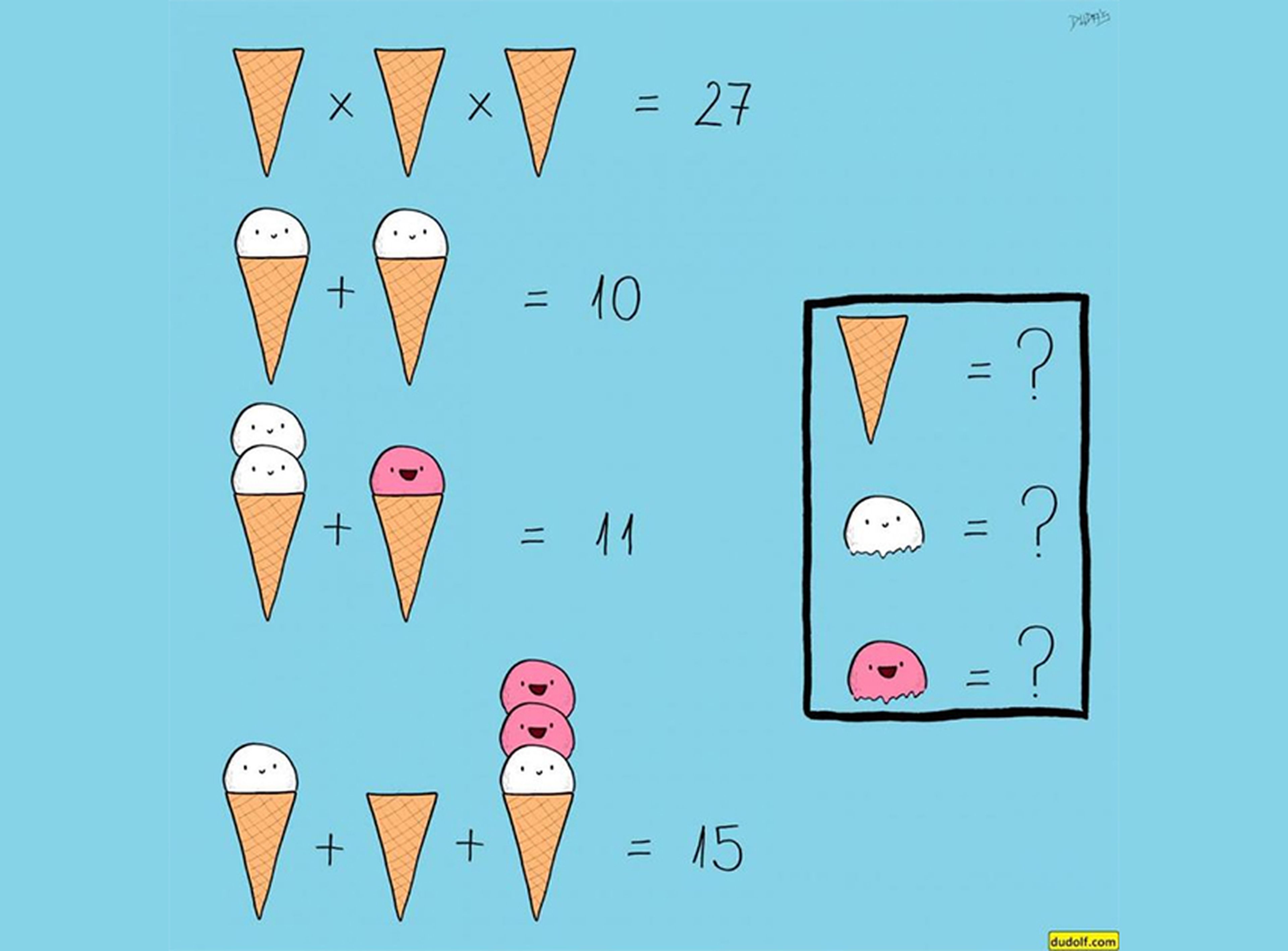
- Algunas personas han tenido éxito al tratar de resolver problemas de matemáticas virales este año.
- Sin embargo, algunos padres tuvieron problemas para resolver los deberes de sus hijos.
- Un matemático británico presentó una solución a un problema matemático de 160 años de antigüedad que le podría hacer millonario.
Internet parece tener una relación de amor odio con las matemáticas.
La gente no tuvo suficiente con los problemas de matemáticas este año así que debatieron sus respuestas en hilos de Twitter y foros de padres. Pero también se lamentaron del dolor de cabeza que les causaron algunos problemas complicados.
Aquí 11 tienes problemas matemáticos, rompecabezas, y acertijos que se hicieron virales este año.
Tan solo el 2% de las personas pudieron resolver este acertijo en menos de 60 segundos.

Adam Spencer, un cómico, matemático y autor de The Number Games, creó un acertijo que tan sólo el 2% de las personas pueden resolver en un minuto, según Reader's Digest.
Escribió los números del 1 al 19 en un orden numérico:
8, 18, 11, 15, 5, 4, 14, 9, 19, 1, 7, 17, 6, 16, ?, ?, ?, ?, ?
Para resolver el acertijo, necesitas averiguar cómo ordenó los primeros 14 números y finalizar la serie añadiendo los últimos cinco.
Los cinco número que faltan son 2, 3, 10, 12 y 13. El patrón es que los números están ordenados por orden alfabético.
La serie completa de números sería así:
8, 18, 11, 15, 5, 4, 14, 9, 19, 1, 7, 17, 6, 16, 10, 13, 3, 12, 2
Este problema chino de matemáticas para niños dejó perplejos a los adultos.

Un problema de matemáticas para niños de primaria en el distrito chino de Shunqingdejó perplejos a adultos de todo el mundo.
El problema sería así: "Si un barco tiene 26 ovejas y 10 cabras a bordo, ¿qué edad tiene el capital del barco?"
¿Cómo se supone que la carga de un barco de ayuda a deducir la edad del capital?
Internet tuvo mucho que decir sobre este aparentemente imposible problema matemático, que se convirtió en trending topic en Twitter.
Después de que la pregunta se hiciera viral, el Departamento de Educación de Shunqing lanzó un comunicado diciendo que la pregunta estaba destinada a medir "la conciencia crítica y la habilidad de pensar independientemente", según la BBC.
Este problema de segundo de primaria dejó a internet confuso

La pregunta es: "Hay 49 perros inscritos en la competición canina. Hay 36 perros pequeños más que perros grandes inscritos para competir. ¿Cuantos perros pequeños se han inscrito para el concurso?"
El razonamiento popular era que si hay 49 perros en total y hay 36 perros pequeños más que grandes, le restarían 36 a 49. Según esa medida, hay 13 perros grandes y 36 perros pequeños, lo que significaría que la respuesta es 36. Pero al ver que esto implicaría que hay 23 perros pequeños más que perros grandes, no dan las cuentas.
El profesor que dio la respuesta más tarde dijo a Popsugar, "El distrito lo explicó mal". Pero tal y como está explicado, la respuesta es 42.5: 49 - 36 = 13, 13 / 2 = 6.5, y 36 + 6.5 = 42.5. Según parece, medio perro se inscribió al concurso.
La gente no se puso de acuerdo sobre la solución a un problema sobre la compra y venta de caballos.

La usuaria de Mumsnet, PeerieBreeks, compartió el acertijo en la web para padres, donde alcanzó cerca de 500 comentarios con otros usuarios debatiendo la respuesta.
Esta es la pregunta: "Un hombre compra un caballo por 60$. Vende el caballo por 70$. Después vuelve a comprar el caballo por 80$ y lo vende, otra vez, por 90$. Al final, ¿cuánto dinero ganó o perdió el hombre? ¿O está en bancarrota?"
Las respuestas en Mumsnet oscilaron entre 10$, 20$ o 30$ hasta la bancarrota. ¿Pero cuál es la solución?
Lo que parece que la gente está ignorando es el hecho de que el hombre vende el caballo por 70$ y después lo compra por 80$, por lo que parece que gastó 10 $ más. Pero la forma correcta de resolver el problema es pensar en las dos transacciones por separado: -60 + 70 = 10 and -80 + 90 = 10.
El hombre gana 10$ con cada venta, por tanto, gana 20$.
El autor Ed Southall compartió un problema de matemáticas en Twitter que algunas personas lograron resolver
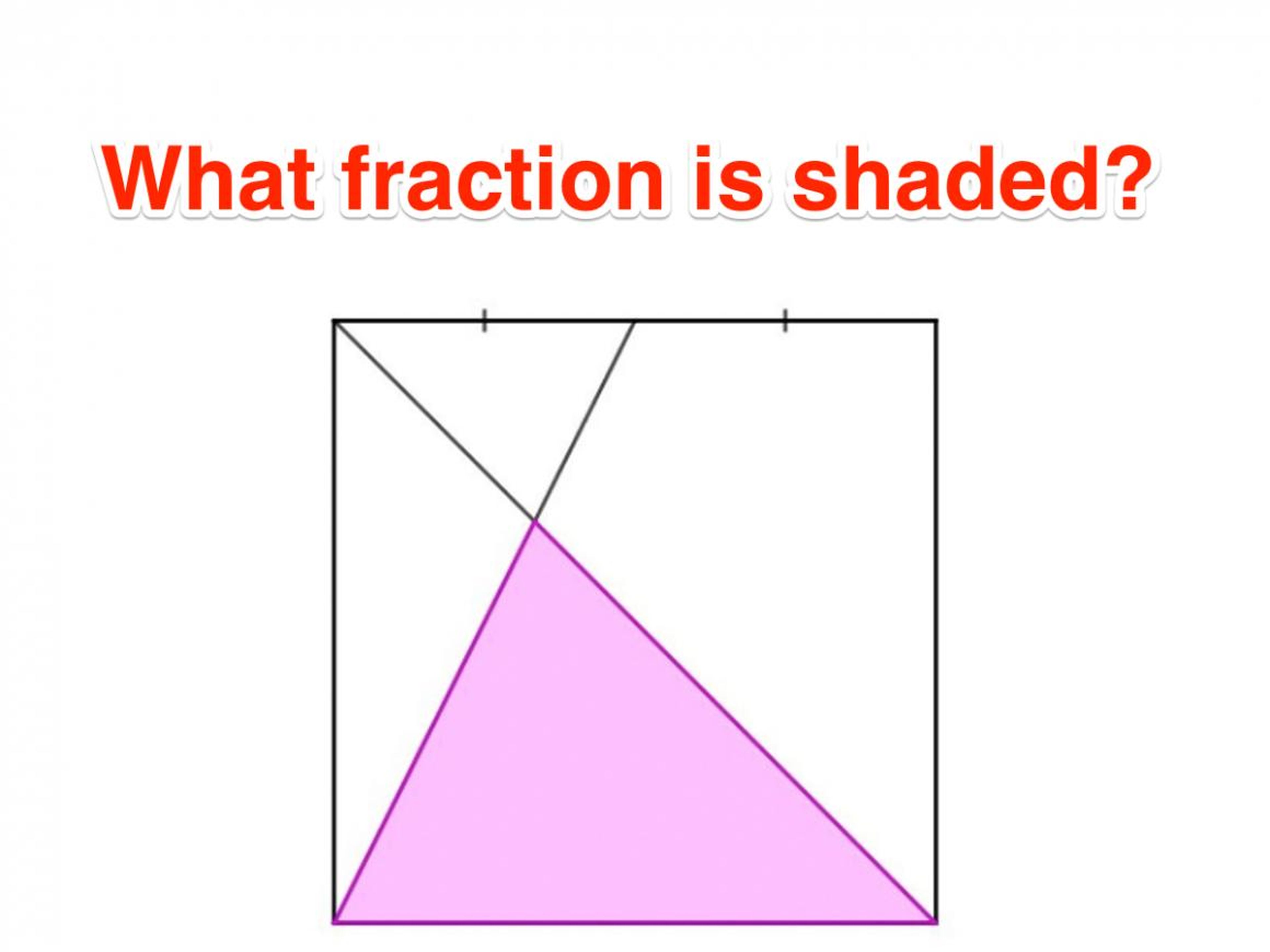
Ed Southall, autor de Geometry Snacks, compartió una foto de un triangulo rosa dentro de un cuadrado y retó a la gente a averiguar tiene un color rosado sombreado. Algunos usuarios de Twitter abandonaron al instante pero otros aceptaron el reto.
Según el reportero de Business Insider, Andy Kiersz, la clave para resolver el problema es la altura del triángulo rosa.
El área de un triángulo es 1/2 (base x altura). Si asumimos que el cuadrado es una unidad de 1x1, podemos ver que la base del triángulo rosado es 1, la longitud del cuadrado. Todo lo que necesitamos averiguar es la altura.
"La clave es que el pequeño triángulo en la parte superior es similar al triángulo rosado, lo que significa que el triángulo pequeño es solo una versión más pequeña del triángulo rosado", dijo Kiersz.
"Una propiedad de los triángulos equiláteros es que la proporción de las alturas de los triángulos será la misma que la proporción de sus bases", dijo. "Dado que la base del triángulo rosa es el doble de la base del triángulo pequeño, su altura también es el doble de la altura del triángulo pequeño. Pero sabemos que la altura del triángulo pequeño más la altura del triángulo rosa es 1, lo que significa que la altura del triángulo rosa es 2/3 . Echas cuentas y obtenemos el área = 1/2 x base x altura = 1/2 x 1 x 2/3 = 1/3 ".
Southall confirmó que la respuesta es, en efecto, 1/3.
Un problema de matemáticas para niños de 8 años se hizo viral cuando los padres no pudieron resolverlo

EL usuario de Mumsnet, lucysmam, fue a internet en busca de ayuda con los deberes de matemáticas de sus hijas.
El problema decía lo siguiente
"En la costa hay tres faros
- La primera luz brilla durante 3 segundos, y luego se apaga durante 3 segundos.
- La segunda luz brilla durante 4 segundos, y luego se apaga durante 4 segundos.
- La tercera luz brilla 5 segundos, y luego se apaga durante 5 segundos.
- Las tres luces se acaban de encender a la vez.
- ¿Cuándo será la primera vez que las tres luces se apaguen al mismo tiempo?
- ¿Cuándo será la próxima vez que las tres luces se enciendan al mismo tiempo?
Afortunadamente, el experto en matemáticas de YouTube Presh Talwalkar ofreció una explicación en su canal, MindYourDecisions.
Según Talwalkar, la forma más sencilla de responder a la primera pregunta acerca de cuándo las luces se apagarán a la vez es hacer un mapa de los intervalos para cada faro y ver cuando sus tiempos de apagado se superponen. La respuesta: después de cinco segundos, cuando la tercera luz, cuando la tercera luz acaba de apagarse y la primera y la segunda luz aún están apagadas.
Para determinar cuando se encenderán de nuevo todas las luces a la vez, debes encontrar el mínimo común múltiple de los intervalos en los que las luces se encienden. La respuesta a esta pregunta es que las luces de los faros se encenderán todas a la vez tras 120 segundos o dos minutos.
Para una explicación más detallada haz click aquí.
Un problema de matemáticas creado por Gergely Dudás usó conos de helado en lugar de variables.
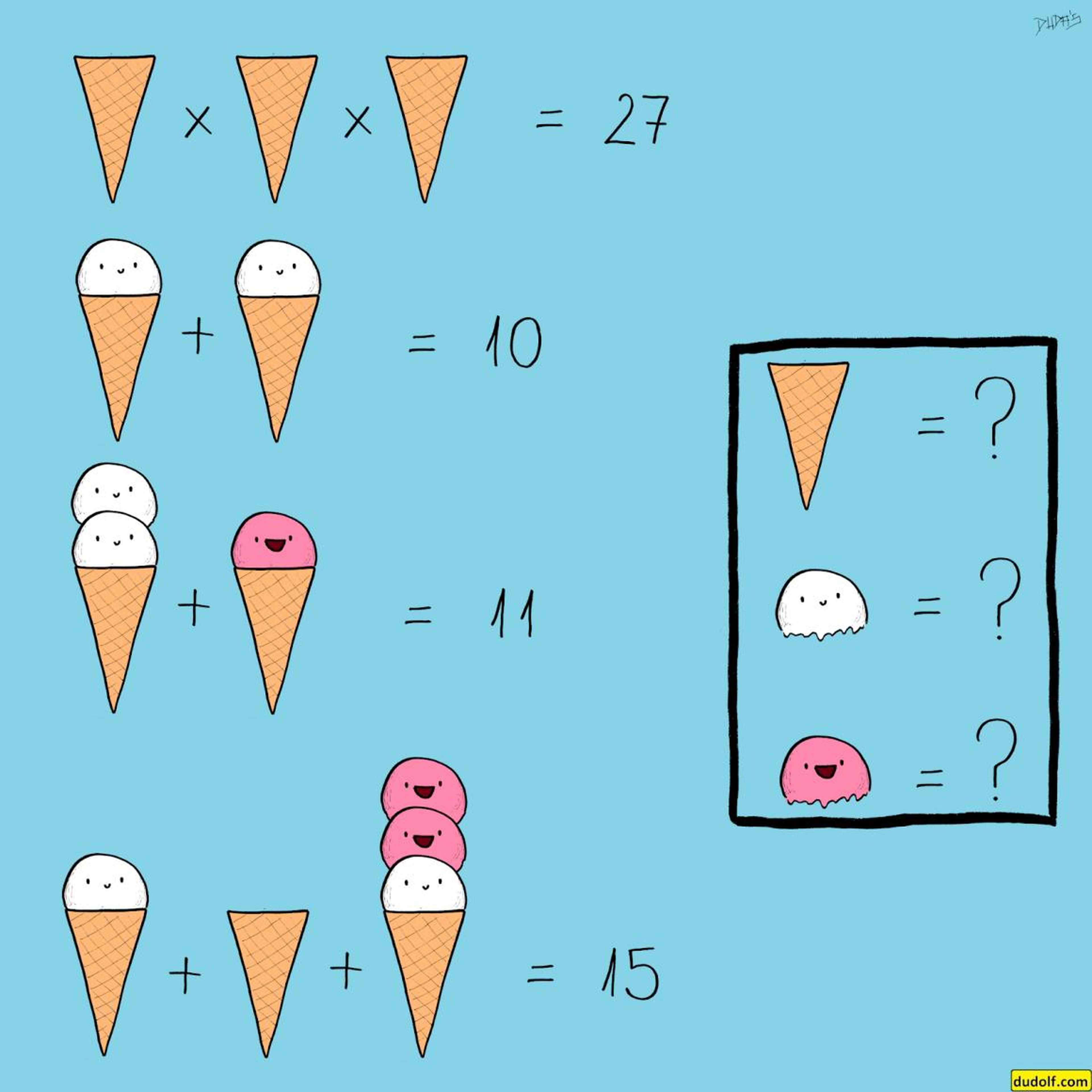
El artista Gergely Dudás, que es conocido por sus complicados puzzles y rompecabezas con objetos ocultos, compartió un problema de matemáticas en su página de Facebook que ilustró con conos de helado.
El rompecabezas consta de cuatro ecuaciones matemáticas, cada una de las cuales se añade o multiplica una suma numérica o producto. Sin embargo, en lugar de variables como x o y, el los acertijo sustituye por conos de helado que están vacíos o tienen cucharadas de helado blanco, rosa o ambos.
Para resolver el puzzle, tienes que averiguar qué número de conos de helados, conos con helado blanco y conos con helado rosa representa cada uno.
La respuesta es que el cono helado vacío representa el número 3, el cono con helado blanco representa el número dos y el cono con helado rosa representa el número uno.
Un hilo de Quora de preguntas difíciles de matemáticas incluía una que la gente llamó "el problema más cruel de todos los tiempos".

Un hilo de Quora de los problemas de matemáticas más difíciles, una de las preguntas salió como "el problema más cruel de todos los tiempos."
Dice así:
- En una clase de p estudiantes, la media (aritmética) de las puntuaciones delos exámenes es 70.
- En otra caso de n estudiantes, la puntuación media para los mismos exámenes fue de 92.
- Cuando se combinan las puntuaciones de las dos clases, la media de la nota del examen es 86.
¿Cual es el valor de p/n?
Talwalkar compartió la solución paso por paso al problema en un vídeo de Youtube.
Hay varias maneras de resolverlo, pero Talwalkar presentó un atajo simple.
La primera clase tiene una media de 70. Esto es 16 puntos por debajo de la puntuación media de 86. En otras palabras, 86 - 70 = 16. Como hay p estudiantes en la clase, la diferencia con la media es 16 p.
La segunda clase tiene una media de 92 puntos. Esto es 6 puntos más que la media de 86 puntos. En otras palabras, 92 - 86 = 6. Hay n estudiantes en la clase, así que la diferencia de la media es 6n.
Dado que estas clases tienen una media conjunta (como dice el problema "cuando las puntuaciones de las dos clases se combinan", el déficit de puntos debe ser igual al superávit de puntos. Entonces, 16 p es igual a 6 n.
Al convertir esto en una ecuación, podemos resolver fácilmente que es p/n:
16 p = 6 n
p/n = 6/16, or 3/8.
Un matemático británico dice que resolvió el "problema más importante" en matemáticas después de 160 años, pero aún debe ser revisado por pares.

La hipótesis de Riemann fue postulada en primer lugar por Bernhard Riemann en 1859. Establece que la distribución de los números primos podría seguir un patrón descrito por una ecuación llamada la función zeta de Riemann. Para resolver la hipótesis, necesitas encontrar una forma para predecir la aparición de cada número primo, aunque históricamente los números primos se han considerado distribuidos al azar.
El premio del millón de dólares va para quien pueda probar que la ecuación se aplica a todos los números primos. El matemático británico Sir Michael Atiyah dijo que resolvió el problema de 160 años, pero su solución necesita ser avalada por una revisión por pares (peer review) antes de que pueda llevarse a casa el premio
A este rompecabezas le falta un número

Igual que un Sudoku, este puzzle creado por Puzzles9 consiste en un rectángulo con nueve cuadrados, cada uno contiene un número, excepto para el cuadrado de abajo del todo a la derecha.
Lee las dos primeras filas de números horizontalmente, cada una como un número - 289 and 324.
El patrón es 17 x 17 = 289 y 18 x 18 = 324. Por lo tanto es lógico que la fila inferior sea 19 x 19 = 361. En consecuencia, el número desaparecido es el uno.
Este rompecabezas tiene tres pentágonos, cada uno con un conjunto de cinco números.
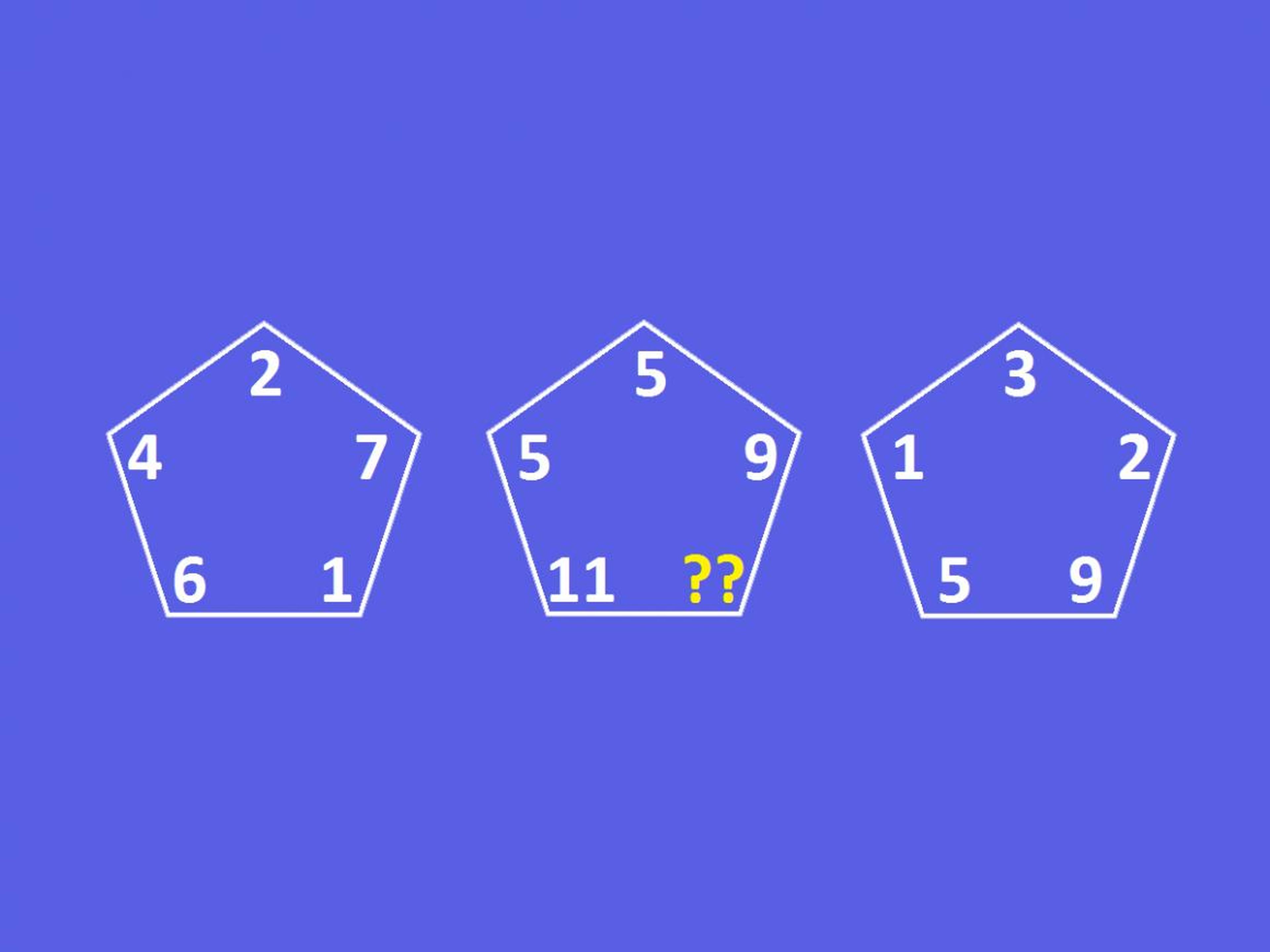
Este rompecabezas creado por Puzzles9 presenta tres pentágonos, cada uno con un conjunto de cinco números. Al pentágono del medio le falta un número en la esquina derecha inferior.
De izquierda a derecha, marquemos los pentágonos como A, B y C. La diferencia entre números en los pentágonos A y B puede encontrarse en el pentágono C en la misma localización en todo el tablero. En otras palabras, Pentágono B - Pentágono A = Pentágono C.
Por tanto, el número que falta es el 10.
Otros artículos interesantes:
Conoce cómo trabajamos en Business Insider.