El concepto matemático que explica tu plan de pensiones y la invasión de los robots

• El crecimiento exponencial es un concepto básico en matemáticas que ocurre cuando una cantidad se duplica una y otra vez.
• Esto puede llevar a un número muy grande muy rápidamente.
• El crecimiento exponencial explica cómo la tecnología se ha desarrollado en las últimas décadas. Al mismo tiempo, es importante tenerlo en cuenta cuando se toman decisiones sobre el ahorro y la inversión.

Uno de los conceptos más omnipresentes en matemáticas, a menudo contrario a la intuición pero que conduce a resultados sorprendentes, es el crecimiento exponencial. El crecimiento exponencial se caracteriza por una cantidad que se duplica en un período de tiempo una y otra vez. Y que lleva a números sorprendentemente grandes muy rápidamente.

Hay una leyenda clásica sobre la invención del ajedrez que ilustra las consecuencias de los exponenciales. Un ministro inventa el juego en la antigua India y se lo presenta a su rey. El rey pide lo que quiere como recompensa y el ministro le pide que coloque un grano de trigo en el primer cuadrado de un tablero de ajedrez, dos granos en el segundo cuadrado, cuatro granos en el tercero, ocho granos en el cuarto, y así sucesivamente para cada uno de los 64 cuadrados en el tablero cuadrado 8x8.

El rey acepta, pero la situación se vuelve insostenible debido a la constante duplicación. En la undécima baldosa del tablero, el rey necesita colocar 1.024 granos de trigo. El día 21, superamos la marca del millón de granos. En el azulejo final del tablero, el rey necesita colocar 9.223.372.036.854.775.808 granos de trigo.

Los números grandes que surgen de los procesos exponenciales hacen que nuestra mente se tambalee. En la vida cotidiana, estamos más acostumbrados a ver cosas que se desarrollan de forma más lineal o subexponencial, por lo que las situaciones de duplicación constante nos despistan.
 

El crecimiento exponencial está frente a nosotros cada día, en nuestras cuentas de jubilación e inversiones

El crecimiento exponencial es clave para ahorrar e invertir. El interés compuesto es un buen ejemplo de un proceso de crecimiento exponencial. Debido a que ganas más gracias a los intereses que ya has ganado, comenzar a ahorrar temprano puede ser muy fructífero.

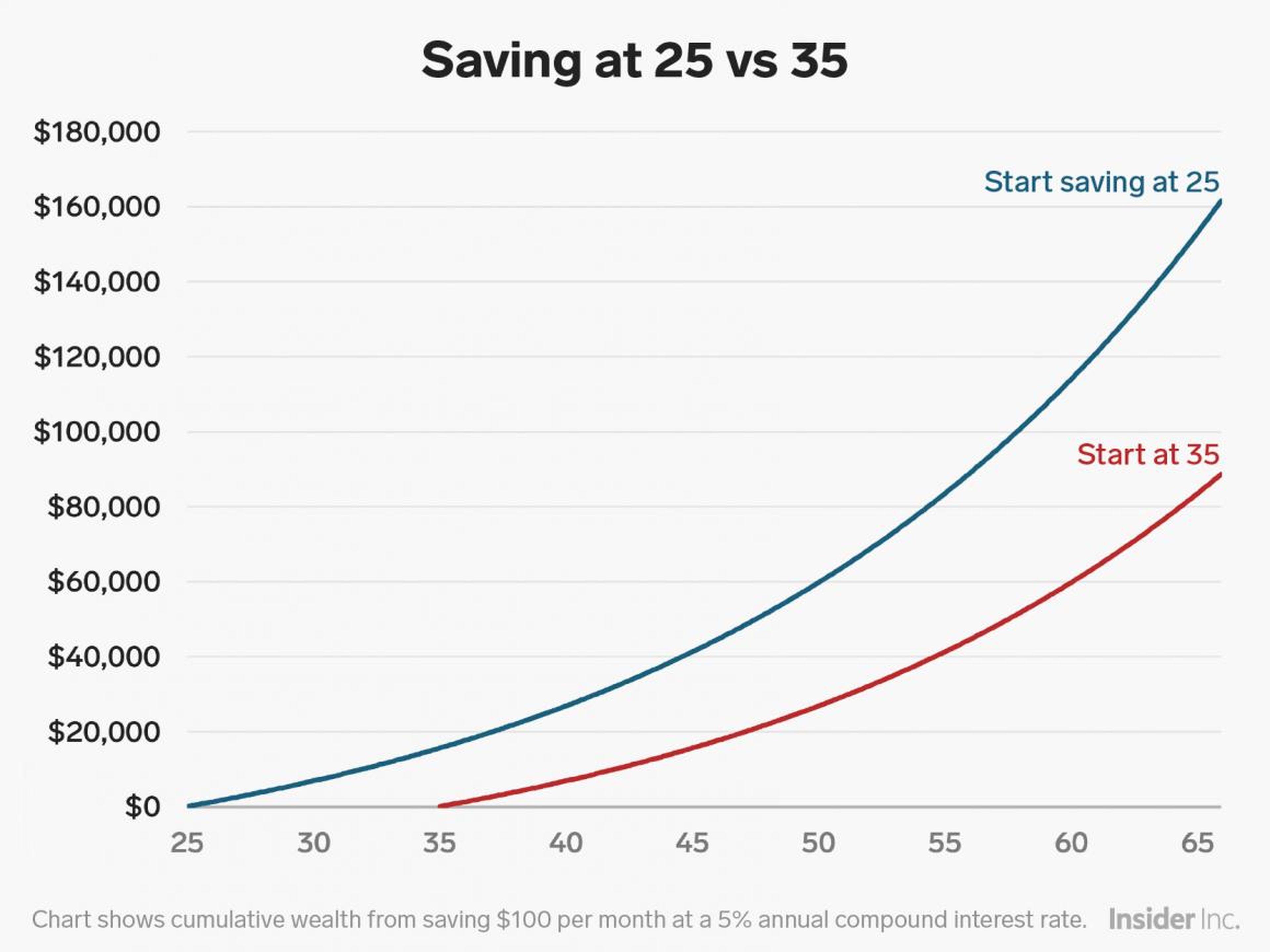
A modo de ejemplo, el siguiente cuadro compara dos ahorradores. Ambos invierten 100 dólares por mes a una tasa de rendimiento compuesto del 5% anual. El primer ahorrador comienza a invertir a los 25 años hasta jubilarse a los 65, mientras que el segundo comienza a ahorrar a los 35. Pero debido a la naturaleza exponencial del interés compuesto, esos diez años adicionales de ahorro significan que, a los 65 años, la primera ahorradora tiene casi el doble en su cuenta que la segunda.

También vemos un crecimiento exponencial de la tecnología

El crecimiento exponencial aparece en muchas situaciones del mundo real. Una de las más famosas es la Ley de Moore de la tecnología. El cofundador de Intel, Gordon Moore, observó en la década de 1960 que el número de transistores que se pueden colocar en un chip de computadora tiende a duplicarse cada dos años. Esa duplicación ha llevado al crecimiento exponencial de la potencia de la computación en las últimas décadas que ha revolucionado la economía global y nuestras vidas.

Otros tecnólogos han generalizado la idea de una tecnología en crecimiento exponencial. El futurista Ray Kurzweil describió una amplia "Ley de Aceleración del Retorno", señalando aumentos exponenciales en otras áreas tecnológicas como la memoria, el almacenamiento en disco duro, las velocidades de Internet y la secuenciación del ADN.

Kurzweil va más allá y sugiere que, si el crecimiento exponencial de la tecnología continúa, la tasa de cambio podría llegar a ser tan rápida que escapara a nuestra comprensión. Esto se conoce como "singularidad tecnológica".

Kurzweil predijo que "no es cierto que vayamos a experimentar cien años de progreso en el siglo XXI, sino que seremos testigos del orden de veinte mil años de progreso" (al ritmo actual de progreso).